Matematicas
Dia 1
Matematicas
Vimos un video motivacional el primer dia, creo que era sobre un entrenador haciendo que su alumno diera todo de si, pero vendado, y lo logro.
Despues de eso tuvimos que hacer una historieta de como creiamos que aparecieron las matematicas, cuando terminamos, nos hablo de los numeros naturales.
Los numeros naturales
Antes de que surgieron los numeros el ser humano se las ingenio para poder hacer varios trazos en piedras, o otras cosas, como en mesopotamia se trazaban en la arena todas sus operaciones
Desde los tiempos primitivos, el hombre ha sentido la necesidad de. aunque haya sido dificil de decir como se ha dicho cuales son os numeros o como le hicieron, era casi como cuando no tienes idea de como empezar a hablar.
Definicion de numero
En matematicas los codigos son diferentes, se empiexan con numeros y despues siguen, numeros negativos, significa relacionado al aprendizaje
nos dijo de lo que significa cada parte de la matematica
calidad referida a las magnitudes (geometria)
a los numeros (aritmetica)
y a ambos (algebra)
ciencia de las relaciones espaciales y cuantitativas
Numeros naturales
0,1,2,3,4,5,6,7
-1= negativo 1= positivo
Propiedades de la multiplicacion
Asociativa, Elemento neutro, comunicativa, distributiva
La adicion en los numeros naturales
Asociativa
Agrupa los elementos de la suma (a + b)+ c = a +(b + c)
Elemento neutro
En la suma es 0 7 + 0 = 0
Comunicativa
Si a, b son numeros naturales cualesquiera, se cumple que a + b = b + a
Dia 2
Propiedades de la sustracion de numeros naturales
Igual que la suma de la resta es una operacion que se derive de l operacion de contar
Propiedades de la multiplicacion de numeros naturales
Asociativa, conmutativa elemento neutro.
distributiva del producto respecto de la suma
Si a,,c son numeros naturales cualesquiera se cumple que
a (b + c) = (a) (b) + (a) (c)
Propiedad de la division de los numeros naturales
La casa de la division se llama Galera
348 + 654 = 1002 852 + 658 = 1510
Dia 3
Elemetos de las operaciones basicas
El maestro nos habia dejado de tarea que teniamos que hacer un cuadro y donde teniamos que poner los elementos de la peracion basica.
Suma: sumados, signo, suma o total
Resta: minuendo, sustraendo, signo, diferencia
Multiplicacion: factor, factor, signo, producto
Division. Cociente, dividendo, divisor, residuo, galera
Propiedades de la suma y la multiplicacion
El maestro tambien nos dejo de tarea poner sobre las propiedades de estas dos operaciones
la propiedad asociativa
Indica que, cuando existen tres o mas cifras en estas operaciones, el resultado no depende de la menra en que se agrupan.
(2 + 6) + 4 = 2 + (6 + 4)
8 + 4 = 2+10
12 = 12
La propiedad conmutativa
Es decir que cuando tienes que resolver una suma, o multiplicacion, no importa como tu lo coloques, siemore obtendras el miso resultado.
4 + 2 = 6 2 + 4 = 6
La propiedad del elemento neutro
Dice que para cualquier numero al que se sume o se multiplique dara el mismo resultado
suma: 0 multiplicacion; 1
4 + 0 = 0 5 x 1 = 0
La propiedad distributiva
Nos afirma que la multiplicacion del dicho numero pr cada una de los sumadores o bueno cuando los numeros se suman pueden dar el resultado de la multiplicacion o viceversa
3 ( 4 + 1 ) = ( 4 + 1) ( 4+1 ) ( 4 + 1 ) ( 4 + 1 )
Dia 4
Pescomposicion de un numero de sus factores primos
multiplicacion y submultiplos
El multiplo de un numero es resultado de dicho numero por cualquier otro numero
5,10,15,20,25,30,35,40,45,50,55,60,65,70,75
12,24,36,48,60,72,
Divisor o submultiplo
Son todos aquellos numeros naturales que me dividen a otro numero natural en forma excelente
1 = 1 unitario 5 = 1,5 Primo
2 = 1,2 Primo 6 = 1,3,6 compuesto
3= 1,3 Primo 7 = 1,7 Primo
4= 1,2,4 compuesto 8 = 1,4,8,2 compuesto
Numero primo es aquel numero que solo tiene 2 el mismo y la unidad
Numero compuesto es aquel numero que tiene mas de dos divisores
El numero 1 recibe el numero de unitario
Despues de eso hicimos un cribo
Divisibilidad entre dos
Un numero tiene division exacta entre 2 cuando su ultima cifra sea 0 o par entre dos: 0,2,4,6,8
Divisibilidad entre tres
Para saber si un numero se divide entre 3 se tienen que sumar todas sus cifras, y si el resultado da un multiplo de 3
Divisibilidad entre 5
Entre 5 el ultimo digital de la cifra tiene que ser 0 o 5
Divisibilidad entre 4
Entre 4 el ultimo digito de la cifra tiene que ser divisible entre 4
Divisibilidad entre 6
Tiene que ser divisible por 2, 4,6,8 y que al mismo tiempo la suma de todos sus digitos es un multiplo de 6.
Despues vimos un video motivacional sobre la pelicula de En busca de la felicidad 💖
Dia 5
MÍNIMO COMÚN MÚLTIPLO
¿Qué es el mínimo común múltiplo?
El mínimo común múltiplo de dos o más números es el múltiplo más pequeño que esos números tienen en común.
El mínimo común múltiplo se suele expresar con las siglas m.c.m. (a, b), siendo a y b los números.
¿Cómo se calcula el mínimo común múltiplo, m.c.m?
Vamos a aprenderlo con un ejemplo, calculamos el mínimo común múltiplo de 180 y 324.
m.c.m. (180,324) 1. Para calcular el mínimo común múltiplo de dos o más números, empezamos por descomponer esos números en factores primos.m.c.m. (180,324)= 22x5x34 El 2 aparece como factor primo en ambas descomposiciones, en ambos casos está elevado a 2. El 5 sólo aparece en la descomposición de 180, pero tenemos que coger todos. El 3 aparece como factor en ambas descomposiciones, pero cogemos el denominador más elevado. 3. Hacemos la multiplicación y obtenemos el mínimo común múltiplo. m.c.m. (180,324)= 22x5x34= 1620 |
MÁXIMO COMÚN DIVISOR
El máximo común divisor de dos o más números es el número más grande por el que se pueden dividir dichos números.
El máximo común divisor se suele expresar con las siglas M.C.D. (a,b), siendo a y b los números.
¿Cómo se calcula el máximo común divisor (M.C.D)?
Vamos a aprenderlo con un ejemplo, calculamos el máximo común divisor de 180 y 324.
M.C.D. (180,324)
1. Para calcular el máximo común divisor de dos o más números, empezamos por descomponer esos números en factores primos.
2. El máximo común divisor se obtiene cogiendo solo los factores primos comunes a los números que hemos descompuesto, elevados al menor exponente. Es decir cogemos solo los factores comunes y los que se repitan los cogemos elevados a la mínima potencia.
M.C.D. (180,324)= 22x32
El 2 aparece como factor primo en ambas descomposiciones, en ambos casos está elevado a 2.
El 3 aparece también como factor común pero en este caso cogemos elevado a la mínima potencia.
El 5 no le cogemos porque no es un factor común.
3. Hacemos la multiplicación y obtenemos el máximo común divisor
M.C.D. (180,324)= 22x32= 36
EJEMPLO. Calculamos el mcm y el MCD de 96, 240 y 180
1. Descomponemos
2. Escogemos los factores
m.c.m. (180,96, 240)= 25x5x32
El 2 aparece como factor primo en ambas descomposiciones, el mayor exponente es 5.
El 5 aparece en la descomposición de 180, y 240 pero tenemos que coger todos.
El 3 aparece como factor en ambas descomposiciones, pero cogemos el denominador más elevado.
M.C.D. (180,96, 240)= 22x3
El 2 aparece como factor primo en las 3 descomposiciones, el menor exponente es 2.
El 3 aparece también como factor común pero en este caso cogemos elevado a la mínima potencia.
El 5 no le cogemos porque no es un factor común.
3. Calculamos
m.c.m. (180,96, 240)= 25x5x32=1440
M.C.D. (180,96, 240)= 22x3= 12
Numeros enteros
Positivos
Negativos
Cero
En la recta numerico el origen es 0
En general:
El valor absoluto de un numero entero positivo es el mismo numero
Todo numero tiene un opuesto 7 -7
Operaciones con los numeros enteros
Adicion con nueros enteros
Son numeros positivos 4 + 2= valor absoluto de 4 es 4 valor absoluto de 2 es 2 y el resultado es 6
Si tengo ( -8 ) + ( -10 ) = -18
Cuando tenemos numeros con diferente signo se van a RESTAR sus valores absolutos pero el signo resultante va a ser el del mayor
-10 el valor absoluto es 10 o el opuesto
( -15 ) + ( 10) = -5
Suma con numeros enteros
Ley de los signos
( + ) ( + ) = + ( - ) ( - ) = + ( - ) ( + ) = - ( + ) ( - ) = -
La ley de los signos es para la multiplicacion y division
Division con numero naturaless y enteros
24 / 6 = 4 12/ 4 = 3
Potencia y raiz cuadrada en nueros enteros
La potencia de un numero consiste en multiplicar a l base del numero de veces que nos indica el exponente.
( 2 )2 = ( -2 ) ( -2) = 4
Numeros racionales
Concepto de fraccion: Parte dividida o separada de un todo considerada por separado.
Concepto de numero decimal: Concepto matemático que expresa una cantidad con relación a la unidad de cómputo; resulta de contar los elementos que forman un conjunto.
Concepto de fraccion propia: Fracción en la que el numerador es menor que el denominador.
Concepto de fraccion impropia: Fracción en la que el numerador es mayor que el denominador.
Conepto de fraccion mixta: Las fracciones mixtas (también llamadas números mixtos o fracciones con enteros) son la suma de un número entero y una fracción propia. Es más fácil ver el significado de la fracción mixta de la siguiente manera. Una fracción mixta es una cantidad de unidades enteras más la parte de otra unidad.
Concepto de fraccion aparente:Fracciones aparentes son aquellas cuyo numerador es múltiplo del denominador. Si dividimos el numerador por el denominador obtenemos un número entero.
Despues de buscar todas las definciones de esto, hicimos un esquema.
Operaciones con nomeros racionales
Suma o adicion
on igual denominador
el numero se suma y se pasa el denominador
Propiedades para la suma de fracciones y decimales
Propiedad conmutativa
La suma de dos fracciones cualesquiera no depende del orden de los sumados. Esto significa que podemos sumar fracciones en el orden que queramos
a / b + c / d = c / d + a / b
Propiedad asociativa
La suma de varias fracciones no depende del orden en que se asocian. Esto significa que cuando tenemos sumas de varios fracciones podemos empezar a sumar las fracciones por donde nosotros queramos
( a / b + c / d ) + m /n = a / b ( c / d + m / n )
Elemento neutro para la suma
El elemento neutro para la suma de fraccion es el cero porque si a cualquier fraccion le sumamos el cero, obtenemos la misma fraccion.
a / b + 0 = a / b
Elemento Las fracciones opuestas o simetricas son fracciones que si se suman el resultado es cero.
a / b = - a / - b = 0
Operaciones con numeros racionales
Suma de fracciones con iguales denominadores
En este caso solamente se suman los numeradores tomando en cuenta sus signosy se recorre el mismo denominador
a / b + c / b = ac / b
Suma de fracciones con diferente denominador
a / b + c / b = bc +ad / bd = bcad / bd
Para resolver estas operaciones tenemos que hacer el metodo de la mariposa para suma de fracciones
Fracciones operaciones de suma o resta}
La suma o resta se resuelve a traves del metodo de la mariposa
En la multiplicacion se multiplica el denominador se multiplica con numerador y viceversa
En la division se multiplica el denominador con el denominador y el numerador con el denominador
Los numeros reales
En matematicas, el conjunto de los numeros reales incluye tanto a los numeros racionales, (positivos, negativos y el cero) como a los irracionales y en otro enfoque, transcedentes y algebraicos. Los irracionales, los trascedentes y algebraicos.
Numero racionales:
-3 / 4 , 5 / 8
Numeros enteros:
-7, -1, 0, 5, 20
Numeros irracionales:
- √5. 2.2360679775.
- √123. 11.0905365064.
- En si los numeros reales incluyen a los numeros naturales o numeros ontables, numeros enteros positivos, negativos y el cero.
- 0, 1, -1, 2, -2, 3, -3
- Propiedades de suma y multiplicacion
- Propiedad conmutativa
- En algebra, la operacion de suma es conmutativa. El orden cual suma soa numeros reales no modifica el resultado no modifica el resultado y como se ve a continuacion
- ( +7 ) + ( + 20 ) = 27
- Identidad aditiva
- La identida aditiva para la s uma de numeros reales es cero
- Inverso aditivo
- El inversa aditivo de la suma es el opuesto del numero real cualesquiera su inverso aditivo es - a
- Propiedad asociativa
- Propiedad clausura
- La propiedad de clausura de la suma de dos numeros reales cualesquiera es un numero real. Si a, b y c son numeros reales, entonces a + b = c.
- Propieda onmutativa
- La propieda conmutativa de la suma estable que el orden en elcual se suman dos nnumeros, no afaecta a la sum. Si a y b son numeros reales, emtonces a ++ b = b + a.
- Concepto de razon
- La comparacion de dos cantidades por medio de una divison.
- En un mercao hay una caja con 20 naranjas, de esas 20, 5 son malas estao significa que
- 20 es el total 5 son malas 0.25 = 25%
- 5 / 20 = 1 / 4 de cada 4 naranjas una es mala
- La compararcion de dos cantidades por medio de una division
- Razones y Proprciones
- Razon: Cociente entre dos numeros o cantidades comparables entre si
- Igauladad entre proporciones El producto de los factores tiene que dar el mismo resultado
- Proporcionalidad directa: Mientras una antidad aumenta, la otra tambien, por si disminuye una cantidad la otra tambien
- Regla de 3: Dos magnitudes son inversamente proporcionales si al omentar una disminuye la ootra en la misma proporcion
- Estadisticas
- Concepto de estadistica: Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades.
- Tipos de estadistica;
Tipos de estadística
A continuación se presentan los principales tipos de estadísticas aplicadas en diversos estudios.
Estadística descriptiva
La estadística descriptiva o deductiva permite presentar de manera resumida y organizada los datos numéricos obtenidos tras un estudio o análisis en particular. Su objetivo, por lo tanto, es describir las características principales de los datos reunidos y evitar generalizaciones.
Estadística inferencial
La estadística inferencial o inductiva es el estudio que utiliza técnicas a partir de las cuales se obtienen generalizaciones o se toman decisiones en base a una información parcial o completa obtenida mediante técnicas descriptivas.
Su objetivo es extraer conclusiones de utilidad sobre el total de las observaciones posibles basándose en la información obtenida.
Estadística aplicada
La estadística aplicada hace uso de los métodos expuestas anteriormente, y permite realizar inferencias a partir de una o varias muestras de una determinada población como objeto de estudio. De esta manera se pueden ofrecer resultados tanto específicos como generalizados.
La estadística aplicada se utiliza en diversas ciencias, como la historia, la economía, la educación o la sociología para realizar estudios y análisis estadísticos.
Estadística matemática
Se trata de la estadística que arroja datos aleatorios e inciertos, por ello hace uso de la teoría de la probabilidad, una rama de las matemáticas que estudia estos casos.
Probabilidad estadísticLa probabilidad estadística es una forma de medición de la certidumbre que asociada a la observación u ocurrencia de un fenómeno o al hecho de que una característica de un objeto de estudio adopte cierto valor. Se puede simplificar dividiendo el número de ocurrencias de un hecho entre el número total de casos posibles.
- Objeto de estudio de la estadistica: El objetivo básico de la estadística es hacer inferencia acerca de una población con base a la información contenida en una muestra (vea las figuras al final de esta sección). ... Definido este número de jóvenes a los cuales, mediante técnicas de consulta adecuadas, se entenderá como una muestra de la población en estudio.
- Conceptos y / o elementos que utiliza la estadistica
Elementos de la Estadística
- Universo o población: esto representa al total del conjunto de objetos o elementos de los cuales se quiere conseguir información. Por lo tanto, el término tiene un significado más extenso que el usual, debido a que puede representar a cosas, actos, áreas geográficas, personas e inclusive el tiempo. Es importante que la población está afinadamente determinada en el espacio y en el tiempo, de manera que ante la figura de un potencial componente de la misma, se pueda concluir si forma parte o no de la población bajo análisis. Consecuentemente, al detallar una población, se debe preservar que el conjunto de manuales que la conforman quede cabalmente delimitado. Por ejemplo, si se está analizando las escuelas de secundarias, se debe detallar cuáles y cuándo: escuelas secundarias de la Capital Federal en el año 1993. Asimismo, se puede afirmar que el tamaño de una población viene dado por el conjunto de elementos que la conforman.
- Unidad de análisis: es el objeto del cual se quiere adquirir información. Varias veces se hace informe a los mecanismos de observaciones con el nombre de elementos. En estadística, una unidad o aparato de análisis puede ser algo con presencia efectiva, como un apartamento o un autobús, o algo más neutro como la temperatura o un descanso de tiempo. Dada esta tesis, puede rediseñar la población como el conjunto de módulos de análisis
¿Que es una grafica?- Un gráfico es una representación visual figurativa que describe conceptos y relaciones. Los gráficos estadísticos plasman datos conceptuales o numéricos y muestran la relación que estos datos poseen entre sí.
- ¿Para que se utiliza una grafica en estadistica?
- Comúnmente son utilizadas para representar relaciones funcionales entre variables numéricas o cuando se tiene una cantidad importante de datos estadísticos. ... En general, para representar las gráficas se utilizan recursos como líneas, puntos, vectores, barras, mapas y símbolos.
- ¿En que consiste la grafica de barras?
- Una gráfica de barras tiene barras rectangulares con longitudes proporcionales a los valores que representan. Las gráficas de barras se utilizan para comparar dos o más valores. Las barras pueden ser horizontales o verticales.
- ¿En que consiste la grafica poligonal?
- Es un tipo de gráfico para expresar datos; los intervalos se colocan en el eje X, y las frecuencias en el eje Y, para poder graficar se le aumenta un intervalo con frecuencia 0(cero). Ejemplos de gráficas poligonales.
- ¿Que es un histograma?
- En estadística, un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados.
- ¿En que cosiste la circular o de pastel?
- Un gráfico circular o gráfica circular, también llamado "gráfico de pastel ", "gráfico de tarta", "gráfico de torta"o"gráfica de 360 grados", es un recurso estadístico que se utiliza para representar porcentajes y proporciones. El número de elementos comparados dentro de una gráfica circular suele ser de más de cuatro.
- ¿Que grafica se utiliza para una variable cuantitativa discreta?
- Podemos representar los datos en tres gráficos, diagrama de barras, polígono de frecuencias y gráfico de sectores. Diagrama de barras, usado para variables cuantitativas discretas. En el eje OX se señalan los valores de la variable y en el eje OY los valores de la frecuencia absoluta.
- ¿Que grafica se utiliza para una variable cuantitativa continua?
- Cuando las variables son continuas, utilizamos como diagramas diferenciales los histogramas y los polígonos de frecuencias. Un histograma se construye a partir de la tabla estadística, representando sobre cada intervalo, un rectángulo que tiene a este segmento como base.
- Expresiones algebraicas
- Una Expresion algebraica tiene 4 elementos
- El signo ( + o - )
- El coeficiente ( entero, fraccion, o deciamal )
- Parte literal ( a, b ,c, d, x, y, z )
- El exponente o exponentes ( positivos, negativos o fraccionarios )
- Rerminos algebraicos
- Monomio 1 = 4 abc
- Binomio 2 = 3 hjc + 7 abnv
- Trinomio 3 = 5 ahdbrg + 6 jsbfe + 8 hjkl
- Polinomio 4 o mas= 6 ab + km + 9 mnj + 7 kny
- Lenguaje algebraico
- El cubo de un numero cualquiera x3, a2
- El cubo de un numero menos el triple de otro 2a - 3b
- El cociente de dos numeros cualquiera a / b
- Ley de exponentes
Leyes de los exponentes
¿Cuáles son las leyes de los exponentes?
La potencia o potenciación consiste en la multiplicación de un número por sí mismo varias veces, y se representan gráficamente de la siguiente manera: xy.
El número que se ha de multiplicar por sí mismo es llamado base y el número de veces por el que se ha de multiplicar es llamado exponente, el cual es más pequeño y debe situarse a la derecha y arriba de la base.
Por ejemplo,
Ahora bien, en operaciones de suma, resta, multiplicación y división con una o varias potencias, ¿cómo proceder? Las leyes de los exponentes nos guían para resolver estas operaciones de la manera más simple posible. Veamos.
1) Potencia cero
1) Todo número elevado a la 0 es igual a 1.
Por ejemplo,
x0 = 1
50 = 1
370 = 1
2) Potencia a la 1
Todo número elevado a 1 es igual a sí mismo.
Por ejemplo,
x1 = x
301 = 30
451 = 45
3) Multiplicación de potencias con la misma base
El producto de potencias con base idéntica es igual a una potencia de igual base, elevada a la suma de los exponentes.
Por ejemplo,
24 · 22 · 24 = 2(4 + 2 + 4) = 210
4) División de potencias con la misma base
Cuando se dividen potencias con la misma base y exponentes diferentes, el cociente es igual a otra potencia con la misma base elevada a la suma de los exponentes.
Por ejemplo,
44 : 42 = 4(4 - 2) = 42
5) Multiplicación de potencias con el mismo exponente
El producto de dos o más potencias diferentes con igual exponente es igual al producto de las bases elevado al mismo exponente.
Por ejemplo:
32 · 22 · 32 = (3 · 2 · 3)2 = 182
6) División de potencias con el mismo exponente
El cociente entre dos potencias con base diferentes e igual exponente resulta en el cociente de las bases elevado al mismo exponente.
Por ejemplo,
82 : 22 = (8 : 2)2 = 42
7) Potencia de una potencia
La potencia de una potencia resulta en otra potencia con la misma base elevada al producto de los exponentes.
Por ejemplo:
(83)3 = 8(3 · 3) = 8
Leyes de los radicales
La ley de los radicales se trata de una operación matemática que nos permite hallar la base a través de la potencia y el exponente.
Los radicales son las raíces cuadras que se expresan de la siguiente manera √, y consiste en conseguir un número que multiplicado por sí mismo dé como resultado lo que está en la expresión numérica.
Por ejemplo, la raíz cuadrada de 16 se expresa de la siguiente manera: √16 = 4; esto significa que 4.4 = 16. En este caso no es necesario indicar el exponente dos en la raíz. Sin embargo, en el resto de las raíces sí.
Por ejemplo:
La raíz cúbica de 8 se expresa de la siguiente manera: 3√8 = 2, es decir, 2 ∙ 2 ∙ 2 = 8
Otros ejemplos:
n√1 = 1, ya que todo número multiplicado por 1 es igual a sí mismo.
n√0 = 0, ya que todo número multiplicado por 0 es igual a 0.
1. Ley de cancelación del radical
Una raíz (n) elevada a la potencia (n) se cancela.
Ejemplos:
(n√a )n = a.
(√4 )2 = 4
(3√5 )3 = 5
2. Raíz de una multiplicación o producto
Una raíz de una multiplicación se puede separar como una multiplicación de raíces, sin importar el tipo de raíz.
Ejemplos:
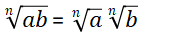
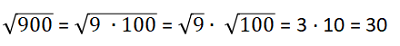
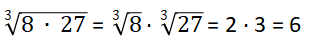
3. Raíz de una división o cociente
La raíz de una fracción es igual a la división de la raíz del numerador y de la raíz del denominador.
Ejemplos:
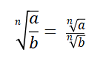
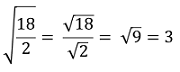
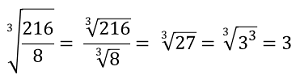
4. Raíz de una raíz
Cuando dentro de una raíz hay una raíz se pueden multiplicar los índices de ambas raíces a fin de reducir la operación numérica a una sola raíz, y se mantiene el radicando.
Ejemplos:
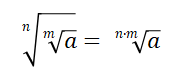
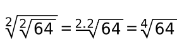
5. Raíz de una potencia
Cuando se tiene dentro de una raíz un número elevado un exponente, se expresa como el número elevado a la división del exponente entre el índice del radical.
Ejemplos:
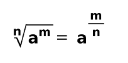
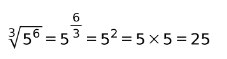 la
la Suma de monomios
A continuación se muestra algunos ejemplos para comprender la suma de monomios de una manera básica:
- Sumar los monomios 4z, 2s y 3p. Ya que el orden de los sumandos no altera la suma, el resultado puede ser:4z + 2s + 3p2s + 4z + 3p3p + 2s + 4z
- Sumar los monomios 3a, 4ab y 2a. Como se puede observar es posible agrupar 3a y 2a, no es posible agrupar 4ab ya que el término no tiene de incógnita las mismas letras (en este caso se tiene la letra b de más). El resultado sería:
3a + 4ab + 2a = 5a + 4ab - Sumar y restar monomios es muy común y normalmente se suele incluir dentro de un paréntesis el sumando negativo, por ejemplo: Sumar los monomios 3a, 6b y –2a.
3a + 6b + (–2a) = 3a + 6b – 2a = a + 6b
Suma de polinomios
Para una mejor representación de la suma de polinomios es recomendable incluir cada polinomio dentro de paréntesis.
- Sumar los polinomios a + 3b, 2a + 3ab y 4b + 2ab.
(a + 3b) + (2a + 3b) + (4b + 2ab) = a + 3b + 2a + 3b + 4b + 2ab Ahora se debe simplificar la anterior expresión algebraica, como resultado será:3a + 7b + 5ab - Sumar los polinomios 3a + 2b y 4b – 2a
(3a + 2b) + (4b – 2a) = 3a + 2b + 4b – 2a Simplificando la anterior expresión, el resultado será:a + 6b
Resta de monomios
A continuación se muestran diferentes ejemplos posibles en la resta de monomios:
- De 6b restar 3b. Determinando el minuendo +6b con su signo y posteriormente el sustraendo +3b con el signo de resta será:
6b – (3b) = 6b – 3b = 3b - De 18c restar 9a. Determinando el minuendo +18c con su signo y posteriormente el sustraendo +9a con el signo de resta será:
18c – (9a) = 18c – 9a En este caso no es posible simplificar ya que cada término tiene diferente letra. - De –13a2b restar 5a2b. Determinando el minuendo –13a2b con su signo y posteriormente el sustraendo +5a2b con el signo de la resta será:
–13a2 – (5a2b) = –13a2b – 5a2b = –18a2b - De –8x2y restar –4ax2. Determinando el minuendo –8x2y con su signo y posteriormente el sustraendo –4ax2 con el signo de la resta será:
–8x2y – (–4ax2) = –8x2y + 4ax2 Se recomienda que el primer término sea el positivo, por lo tanto, es posible reacomodar el resultado de la siguiente manera:4ax2 – 8x2yesta de polinomios
En la resta de monomios en realidad consiste en cambiar el signo del sustraendo, es recomendable analizar con paréntesis ya que en la resta de polinomios el signo de la resta afecta a todo el sustraendo, por lo tanto, se estaría empleando el mismo método realizado.
- De 3x + 4y + 11w restar 2x + 3y + 8w.
3x + 4y + 11w – (2x + 3y + 8w) = 3x + 4y + 11w – 2x – 3y – 8w El resultado después de agrupar los términos semejantes será:x + y + 3w
Para una mejor estructuración se recomienda analizar la resta en un acomodo de columna de modo que los términos semejantes estén uno sobre otro.
- De 5xy2 + 6y + 8w restar 5xy2 + 3y. Ya que el signo de la resta afecta a todo el polinomio se tendría: – (5xy2 + 3y) = – 5xy2 – 3y5xy2 + 6y + 8w–(5xy2 + 3y) 0 + 3y + 8w
Nota: Como se puede observar se emplea suma y resta para la solución de problemas algebraicos.
- De 3xy2 – 5x2y – 8x3 restar 5x2y + 8x3 – 3xy2. Ya que el signo de la resta afecta a todo el polinomio se tendría: – ( 5x2y + 8x3 – 3xy2) = – 5x2y – 8x3 + 3xy2.–5x2y – 8x3 + 3xy2–(5x2y + 8x3 – 3xy2)–10x2y – 16x3 + 6xy2Para comprobar el resultado es el mismo método que la resta en aritmética, la diferencia (resultado) con el sustraendo debe dar el minuendo, por lo tanto, se hace una suma:–10x2y – 16x3 + 6xy2 5x2y + 8x3 – 3xy2 –5x2y – 8x3 + 3xy2Un monomio es una expresión que está formada solamente por un solo término algebraico, como por ejemplo:
- P(x) = 4x²
- j(x,y,z) = 5x3y4z2
- q(x,y) = x³y²
La expresión p(x,y) = x²y + xy, no es un monomio, pues tiene más de un término algebraico.
CÓMO MULTIPLICAR Y DIVIDIR UN MONOMIO
Para lograr efectivamente la multiplicación y división de monomios, primero debemos tener en cuenta el signo, después los coeficientes y por último las potencias.
Ejemplo 1: Multiplicar los siguientes monomios (5x³y) × (- 3y4z)
Recordando la propiedad de la potencia na × nb = na + b, tenemos:
(5x³y) × (- 3y4z) = – 15x3y5z
Ejemplo 2: Realizar la siguiente división de monomios (8x3y3z4t) ÷ (-2xy2z2)
Recordando las propiedades de potencias na × nb = na + b y 1/na = n-a, tenemos:
(8x3y3z4t) ÷ (-2xy2z2) = -4x2yz2t
Ejemplo 3: Multiplicar los siguientes monomios (3x²y) × (7xy).
Recordando la propiedad de la potencia na × nb = na + b, tenemos:
(3x²y) × (7xy) = 21x³y²
Ejemplo 4: Realizar la siguiente división de monomios (6x²y³) ÷ (-2xy).
Recordando las propiedades de potencias na × nb = na + b y 1/na = n-a, tenemos:
(6x²y³) ÷ (-2xy) = -3xy²
Trinomio cuadrado perfecto
Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.
En el trinomio cuadrado perfecto los términos cuadrados son siempre positivos, en cambio el término del doble producto puede ser negativo; en este caso debe ser negativo uno de los términos del binomio cuyo cuadrado es el trinomio dado, del ejemplo anterior tenemos:
Ambas son respuestas aceptables.
Regla para conocer si un trinomio es cuadrado perfecto.
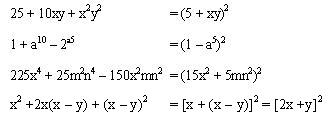 Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.
Un trinomio ordenado con relación a una letra es cuadrado perfecto cuando la primera y tercer letra son cuadrados perfectos (o tienen raíz cuadrada exacta) y son positivos y el segundo termino es el doble producto de sus raíces cuadradas.Factorización
La factorización o descomposición factorial es el proceso de presentar una expresión matemática o un número en forma de multiplicación. Recordemos que los factores son los elementos de la multiplicación y el resultado se conoce como producto.
Tipos de factorización
En líneas generales, podemos hablar de dos tipos de factorización: la factorización de números enteros y la factorización de expresiones algebraicas.
Factorización en números primos
Todo número entero se puede descomponer en sus factores primos. Un número primo es aquel que es divisible unicamente entre 1 y el mismo. Por ejemplo, el 2 solo se puede dividir entre 1 y 2.
Podemos descomponer un número dado X como la multiplicación de sus factores primos. Por ejemplo, el número 525 es igual a la multiplicación de 52.3.7.
Factorización de expresiones algebraicas
El objetivo de la factorización es llevar un polinomio complicado y expresarlo como el producto de sus factores polinomiales simples.
Se llaman factores o divisores de una expresión algebraica a las expresiones algebraicas que multiplicadas entre si dan como producto la primera expresión. Por ejemplo:
Los factores son:
Cómo factorizar
Cuando hablamos de factorizar, podemos seguir las siguientes recomendaciones:
- Observar si hay un factor común, esto es, si hay un factor que se repita en los diferentes términos.
- Ordenar la expresión: a veces al arreglar la expresión nos percatamos de las posibilidades de factorización.
- Averiguar si la expresión es factorizable: en ocasiones estamos en presencia de expresiones que no pueden ser descompuestas en factores.
- Verificar si los factores hallados son a su vez factorizables.
Productos notables
Saltar a: navegación, búsquedaProductos notables es el nombre que reciben multiplicaciones con expresiones algebraicas cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.
Factor común
El resultado de multiplicar un binomio a+b por un término c se obtiene aplicando la propiedad distributiva:
Para esta operación existe una interpretación geométrica, ilustrada en la figura adjunta. El área del rectángulo es
(el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas: ca y cb.
Ejemplo:
Binomio al cuadrado o cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Así:
Un trinomio de la expresión siguiente:
se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:
En ambos casos el signo del tercer término es siempre positivo.
Ejemplo:
Simplificando:
Producto de dos binomios con un término común
Cuando se multiplican dos binomios que tienen un término común, el cuadrado del término común se suma con el producto del término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.
Ejemplo:
Agrupando términos:
Luego:
Producto de dos binomios conjugados
Véase también: Conjugado (matemática).Dos binomios conjugados se diferencian sólo en el signo de la operación. Para su multiplicación basta elevar los monomios al cuadrado y restarlos (obviamente, un término conserva el signo negativo), con lo cual se obtiene una diferencia de cuadrados.
Ejemplo:
Agrupando términos:
A este producto notable también se le conoce como suma por la diferencia.
Polinomio al cuadrado
Para elevar un polinomio de cualquier cantidad de términos se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.
Ejemplo:
Multiplicando los monomios:
Agrupando términos:
Luego:
Binomio al cubo o cubo de un binomio
Para calcular el cubo de un binomio se suman, sucesivamente:
- El cubo del primer término con el triple producto del cuadrado del primero por el segundo.
- El triple producto del primero por el cuadrado del segundo.
- El cubo del segundo término.
Identidades de Cauchy:
Ejemplo:
Agrupando términos:
Si la operación del binomio implica resta, el resultado es:
- El cubo del primer término.
- Menos el triple producto del cuadrado del primero por el segundo.
- Más el triple producto del primero por el cuadrado del segundo.
- Menos el cubo del segundo término.
Identidades de Cauchy:
Ejemplo:
Agrupando términos:
Identidad de Argand
Identidades de Gauss
Identidades de Legendre
Identidades de Lagrange
Artículo principal: Identidad de Lagrange.Otras identidades
Dado que la notabilidad de un producto es un concepto ambiguo, no existe una lista determinante que indique a cuáles productos se les puede considerar notables, y a cuáles no. A otras fórmulas, aunque menos usadas que las anteriores, en ciertos contextos se les puede calificar de productos notables. Entre ellas se destacan:
Adición de cubos:
Diferencia de cubos:
Es más frecuente listar las dos expresiones anteriores como fórmulas de factorización, ya que los productos no tienen una forma particularmente simétrica, pero el resultado sí (contrástese, por ejemplo, con la fórmula de binomio al cubo).
La suma y la diferencia de cubos se pueden generalizar a sumas y diferencias de potencias enésimas (o n - ésimas: xn).
Suma de potencias enésimas:
- Si -sólo si- n es impar,
Diferencia de potencias enésimas:
Las fórmulas de binomio al cuadrado y binomio al cubo se pueden generalizar mediante el teorema del binomio.
Para representar un cubo como suma de dos cuadrados existe una fórmula ingeniosa:
Incógnita: La letra (o variable) que figura en la ecuación.
Miembro: Es cada una de las dos expresiones algebraicas separadas por el signo "=".
Término: Cada uno de los sumandos que componen los miembros de la ecuación.
Grado: Es el mayor de los exponentes de las incógnitas, una vez realizadas todas las operaciones (reducir términos semejantes).
- Que tiene las mismas características que otra persona o cosa en algún aspecto o en todos
1. Ecuaciones Elementos de una ecuación
En las ecuaciones distinguimos varios elementos :
Triángulo de Pascal y números Combinatorios
- Los números del triángulo de Pascal coinciden con los números combinatorios.El número combinatorio Cm n (n sobre m) se encuentra en el triángulo en la fila n+1, en el lugar m+1.El número combinatorio Cm n (n sobre m) que representa el número de grupos de m elementos que pueden hacerse de entre un conjunto de n (por ejemplo, (4 sobre 2) nos da el número de parejas distintas que podrían hacerse en un grupo de cuatro personas), se encuentra en el triángulo en la fila n+1, en el lugar m+1.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
...Podemos saber que el número de parejas posibles que decíamos antes es 6 si miramos el tercer número de la quinta fila.Esto hace que el triángulo sea útil como representación de estos números, y proporciona una buena forma de intuir sus propiedades.Por el contrario, a la fórmula de los números combinatorios se le puede dar el carácter de fórmula general del triángulo para saber, sin necesidad de construir todas las filas anteriores, cuál es el número que ocupa un lugar determinado,:
 Triángulo de Pascal y Binomio de Newtón
Triángulo de Pascal y Binomio de Newtón- La fórmula general del llamado Binomio de Newton (a + b)n está formada por unos coeficientes que coinciden con la línea número n+1 del triángulo de Pascal (la que empieza por 1 y n).La fórmula es:

Una forma de evitar tener que calcular uno a uno todos los coeficientes es utilizar el Triángulo de Pascal, ya que los coeficientes de la potencia n aparecen en la fila n+1 de dicho triángulo.
Un ejemplo: aplicando la fórmula y la definición de número combinatorio tendríamos:(a + b)3 = 1·a3 + 3·a2b + 3·ab2 + 1·b3.Pero hubiese sido más rápido ir a la fila 4 (3 + 1 ) del triángulo y ver que los números que aparecen son, precisamente, los coeficientes 1, 3, 3 y 1.
 Más propiedades del triángulo de Pascal:
Más propiedades del triángulo de Pascal:Lo difícil es mirar este triángulo durante un par de minutos y no encontrarle alguna regularidad oculta.
- Números poligonales¿Podríais decir qué sucesiones son las que forman las diagonales del triángulo? Las primeras de la izquierda y la derecha no son más que unos. Las segunda forman la sucesión de los números naturales... ¿Y la tercera? ¿Y la cuarta?En la diagonal tercera marcada aparecen, pero además en la inmediata inferior aparecen los números tetragonales, es decir, los que forman las pirámides triangulares, cuyos pisos son a su vez números triangulares.se encuentran en el triángulo de Pascal recurriendo a la misma diagonal que en el caso anterior: construimos cada uno sumando dos números triangulares consecutivos. Eso nos proporciona: 1, 4, 9, 16, 25, ...De hecho, por este método recurrente podemos construir todos los números poligonales, y en ese sentido están presentes en el triángulo de Pascal.
- Números primosSi el primer elemento de una fila es un número primo, todos los números de esa fila serán divisibles por él (menos el 1, claro). Así, en la fila 7: (1 7 21 35 35 21 7 1), los números 7,21 y 35 son divisibles por 7.
- La suma de los elementosLa suma de los elementos de cualquier fila es el resultado de elevar 2 al número que define a esa fila. Así:20 = 121 = 1+1 = 222 = 1+2+1 = 423 = 1+3+3+1 = 824 = 1+4+6+4+1 = 16
- Sucesión de FibonacciLa serie de Fibonacci puede ser encontrada también en el triángulo de Pascal. Dividiendo al mismo según las líneas que mostramos en el diagrama, los números atrapados entre ellas suman cada uno de los elementos de esta sucesión.Recordemos que esta sucesión (que, por cierto, se construye de manera similar al triángulo de Pascal), es:1,1,2,3,5,8,13,21,...(an+1 = an + an-1con a0 = 1, a1= 1)
- Potencias de 11Podemos interpretar cada fila como un único número. Si la fila está formada por números de un solo dígito, basta unirlos. En el caso de la fila 2 tenemos:1-2-1............................ 121 = 112Cuando los números de la fila constan de más de un dígito, se "reparten" para formar el número final como se observa en el ejemplo siguiente para la fila 5:1-5-10-10-5-1........... 1-(5+1)-(0+1)-0-5-1=1-6-1-0-5-1 ............ 161051 = 115
- El "stick de hockey"Cualquier diagonal que empiece en un extremo del triángulo, y de la longitud que sea, cumple la siguiente propiedad:La suma de todos los números que la integran se encuentran justo debajo del último de ellos, en la diagonal contraria.
- El triángulo de SierpinskiEl curioso dibujo que se forma al pintar de negro los números impares del triángulo y de blanco los pares, recuerda al triángulo de Sierpinski , uun famoso conjunto geométrico (un fractal determinístico que se puede construir a partir de cualquier triángulo) El applet de Java de esta página muestra inicialmente las primeras filas del triángulo de Pascal. Se puede aumentar el número de filas y se puede elegir entre colorear los números pares o no colorearlos. Cuando se elige colorear se observa perfectamente que al ir aumentando el número de filas el objeto resultante se va aproximando al triángulo de Sierpinski.
- Cambiando extremos
2
1 2
1 3 2
1 4 5 2
1 5 9 7 2
1 6 14 16 9 2
......¿Qué pasaría si cambiamos los unos de uno de los lados externos del triángulo de Pascal por doses ?. ¿Qué relaciones numéricas se pueden encontrar? ¿Qué sucedería si en lugar de doses colocamos treses o cuatros?
Definición del binomio de Newton
El binomio de Newton es la fórmula que nos permite hallar las potencias de un binomio.

Podemos observar que:
El número de términos es
 .
.Los coeficientes son números combinatorios que corresponden a la fila enésima del triángulo de Tartaglia (también conocido como triangulo de Pascal).

En el desarrollo del binomio, los exponentes de van disminuyendo, de uno en uno, de
 a cero; y los exponentes de van aumentando, de uno en uno, de cero a , de tal manera que la suma de los exponentes de y de
a cero; y los exponentes de van aumentando, de uno en uno, de cero a , de tal manera que la suma de los exponentes de y de  en cada término es igual a .
en cada término es igual a .En el caso que uno de los términos del binomio sea negativo, se alternan los signos positivos y negativos
Gracias por su atencion.

Comentarios
Publicar un comentario